Wolfram|Alphaは広範に及ぶ連立方程式を解くことができます.一次連立方程式や非線形方程式を含む連立方程式を解くことができ,整数解や別の領域上の解を求めることもできます.さらに不等式やより一般的な制約条件を含む系を解くこともできます.
WolframAlpha
オンライン連立方程式ソルバ
Wolfram|Alphaで方程式,連立方程式を解く
連立方程式や制約条件を含む系の解を求めるための強力なツール
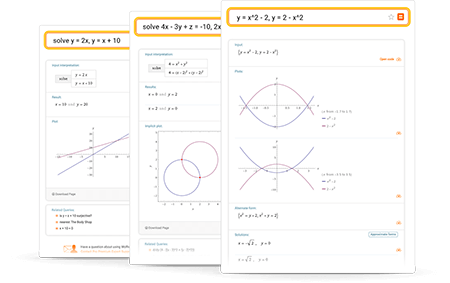
詳細
入力のヒント
平易な言葉を使ってクエリを入力してください.曖昧なクエリを避けるために,必要に応じてカッコを使ってください.以下はクエリ入力の例です.
すぐに使える学習ツールにアクセス
「ステップごとの解説」やWolfram Problem Generatorで即時にフィードバックやヒントを得ることができます
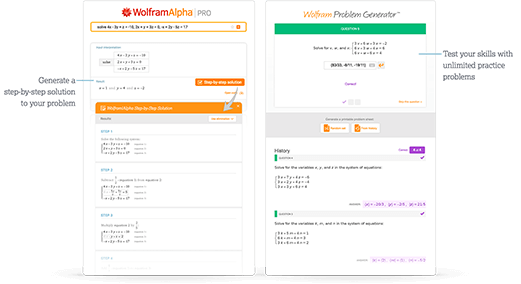
詳細
連立方程式とは何ですか?
連立方程式(方程式系)とは,複数の変数を持つ,複数の方程式の組です.
連立方程式の解は,その方程式すべてが満たされるような変数の値のことです.連立方程式を解くということは,そのような値をすべて見付けることです.
連立一次方程式は,一般的で適用範囲の広い連立方程式です.2変数の場合,一次方程式は二次元空間に描かれた直線と考えることができます.連立方程式が表すすべての直線が共通の一点で交わる場合,その交点の座標が解に相当します.それ以外の場合は,解はありません.3個以上の変数を持つ連立一次方程式も同様で,一つの解を持つ,解がない,無限個の解を持つ(連立方程式を構成するすべての方程式が同等である場合)のいずれかになります.
非線形の関数を含むような,より一般的な連立方程式もあります.これらは,1個,0個,無限個,あるいは任意の数の解を持つ場合があります.さらに進んで,不等式を含むものや特定の変数が整数である等の制約条件を持つ,より一般的な連立方程式も可能です.
連立方程式を解くことは非常に一般的かつ重要な考え方であり,数学,工学,科学の多くの分野における基礎となります.