Wolfram|Alphaは多項式の根を求めたり方程式系を解いたりするのに最適なツールです.多項式の因数分解,多項式の解集合や不等式のプロット等を行うこともできます.
オンライン方程式ソルバ
Wolfram|Alphaで一次,二次,高次方程式を解く
単なるオンライン方程式ソルバではありません
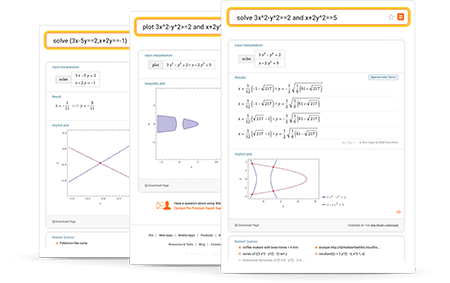
詳細
入力のヒント
平易な言葉を使ってクエリを入力してください.曖昧なクエリを避けるために,必要に応じてカッコを使ってください.以下はクエリ入力の例です.
すぐに使える学習ツールにアクセス
「ステップごとの解説」やWolfram Problem Generatorで即時にフィードバックやヒントを得ることができます
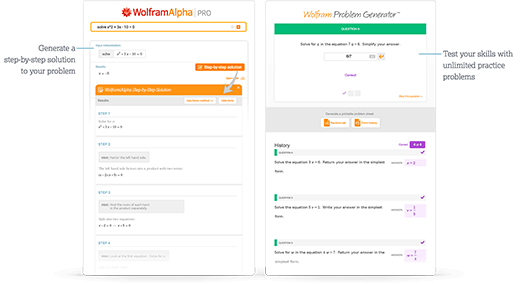
詳細
方程式の解法について
pc=0のとき,値 c を多項式 pxの根と言います.
pxに現れる x の最大の指数を p の次数と言います.pxの次数が n ならば,重複度を考慮に入れると n 個の根があることが知られています.重複度が何かを理解するために,x2 - 6x + 9=x-32=x-3x-3を例に取ります.この多項式には2個の根があると考えられ,その両方が3となります.
有理数であるすべての根を求める方法として,代数学では「因数定理」を学びます.また,すべての二次多項式の根を求める方法として,必要に応じて判別式から生じる平方根を使うやり方も学びます.三次および四次の多項式の根を表すための高度な公式や,任意の多項式の根を近似するための数値解法も多数あります.これらは複素解析や高度な数値アルゴリズムが用いられており,これはまさに現在研究開発が盛んな分野です.
一次方程式系はガウスの消去法またはそれに関連したメソッドを使って解かれることがよくあります.これも通常高校・大学レベルで出てきます.非線形連立方程式の根を求めるためには,もっと高度なメソッドが必要です.不等式系を扱う場合も同様なことが言えます.線形の場合は,線形代数の授業で習ったメソッドを使って解くことができますが,高次の多項式系にはより高度な計算ツールが必要です.
Wolfram|Alphaが方程式を解く方法
方程式を解く場合,Wolfram|AlphaはWolfram言語の関数SolveとReduceを呼び出します.この2つの関数には,基本的な一次方程式や二次方程式から多変数の非線形系まで,あらゆる種類の代数を解くための多岐に渡るメソッドが含まれています.スピードと信頼性を高めるように最適化された,ガウスの消去法のような線形代数メソッドが使われることもあれば,結果を計算するために整数論,抽象代数,その他の高度な分野の定理やアルゴリズムに依存した操作もあります.これらのメソッドは,Wolfram|Alphaが最小限の計算時間でさまざまな問題が解けるように,注意深く設計され選ばれています.
このようなメソッドは,解を直接得るために便利なものですが,人間なら同じ問題をどのように解くかということを理解するためにも重要なものです.このため,Wolfram|Alphaには人間が認識し追跡しやすい典型的な手法を使って,代数操作をステップごとに示すための個別のアルゴリズムが備わっています.これには消去法,代入法,二次方程式の解の公式,クラメールの公式等,多数含まれます.