Wolfram|Alphaは,不定積分,定積分,二重・三重積分,広義積分を計算するのに適したツールです.Wolfram|Alphaの積分計算機はプロット,答の別の形,その他の関連情報も出力するので,数学的直観力を高めることができます.
オンライン Integral Calculator
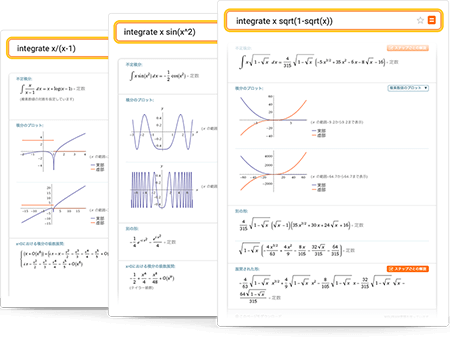
Wolfram|Alphaを使って積分を実行する
単にオンラインで積分を解くだけではありません
詳細
入力のヒント
上の数学入力を使うか,平易な言葉で積分計算機のクエリを入力するかしてください.あいまいな表現を避けるために,必要な箇所には必ずカッコを付けてください.以下は平易な言葉を使った,積分のクエリの例です.
すぐに使える学習ツールにアクセス
「ステップごとの解説」やWolfram Problem Generatorで即時にフィードバックやヒントを得ることができます

詳細
積分とは
積分は微積分の重要なツールで,逆微分を与えたり,曲線の下の面積を表したりすることができます.
f x の不定積分は f xdx と表記され,f x の逆微分と定義されます.つまり,f xdx の導関数は f x ということです.定数を微分するとゼロになるので,任意定数分の不定性を残した形で定義されます.例えば,−cosx + constantの導関数はsinxなので,sinxdx = -cosx+constantになります.x = a から x = b までの f xの定積分は baf xdx と表記され,x = a から x = b までの f x と x 軸の間の符号付きの面積と定義されます.
どちらのタイプの積分も微分積分学の基本定理で結び付けられています.この定理は,「f x がa,bにおいて積分可能であり,Fxがその連続不定積分であるならば,baf xdx = Fb - Faである」というものです.つまり,π0sinxdx = -cosπ - -cos0 = 2ということです.定積分の近似が望ましいこともあります.これを行う場合,曲線の下に細い長方形を置いて符号付きの面積を足す方法がよく使われます.Wolfram|Alphaは多様な積分を解くことができます.
Wolfram|Alphaはどのように積分を計算するのか
Wolfram|Alphaは人間とは異なる方法で積分を計算します.Wolfram|Alphaは,莫大な量の数学的および計算的な研究の成果である Mathematica のIntegrate関数を呼び出します.Integrateは人間のようには積分を計算せず,パワフルな汎用アルゴリズムを使います.このアルゴリズムにはしばしば非常に高度な数学がかかわっています.一般にこの関数が取るアプローチは2つあります.1つ目の方法は,積分の一般形を計算し,この形式を微分して方程式を解き,未定の記号的パラメータにマッチさせるというものです.非常に簡単な被積分関数の場合でも,この方法で生成された方程式は非常に複雑で,Mathematica の強力な代数計算機能を使って解かなければならないことがあります.Mathematica が積分を計算するのに使うもう一つの方法には,積分を一般超幾何関数に変換して,これらの非常に一般的な数学関数についての関係を使うというものがあります.
これらのパワフルなアルゴリズムにより,Wolfram|Alphaは積分を非常に迅速に計算したり,さまざまな特殊関数を扱ったりできるのですが,人間が積分を実行する方法を理解することも重要です.そのため,Wolfram|Alphaには段階を追って積分を実行するアルゴリズムも備わっています.このアルゴリズムは人間が積分を計算する方法を模倣した,全く異なる積分方法を使っています.これには,置換積分法,部分積分法,三角関数による置換積分,部分分数による積分があります.